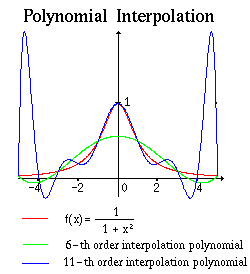
INTERPOLATION
(This is a full windows application, can run on NT4.0 and Win2000, probably on Win98 as well. To run the application, which uses Microsoft Component Object Model and Compaq Array Visualizer to display data graphically, you will need to install Aviewer.exe. Read the instructions in Aviewer.txt for details. You may also need Aview110.dll. These software components are freely distributable with the application. This does not apply to those who have Compaq Visual Fortran 6.2 or higher installed). This also a nice way to write your first windows application in Fortran if you haven't done so already. The Fortran subroutines (F90 style) will be soon available here.
SPLINES
- Cubic spline interpolation (driver routine, binary search routine, interpolation routine, evaluation routine). The driver routine uses not a knot condition; for a proof of convergence, see here. (approx. 90 K)
- Linear systems solvers for general banded matrices (BANFAC, BANSLV), positive definite banded matrices (BCHFAC, BCHSLV) and block-diagonal systems (SLVBLK (FCBLOK (FACTRB, SHIFTB)),SBBLOK (SUBFOR, SUBBAK)). The order in parenthesis implies calling sequence. See coments included at the top of the main program. All routines are F77 style and are together in one compressed file; click here to download
ALGORITHMS FOR MANIPULATING B-SPLINES
A collection of F77 style subroutines by C. deBoor ; click here to download a self-extractable file. Self-explanatory comments included.
GEOMETRIC APPROACH
Self-extractable file containing a scanned document with basics of blossoming (880 K). Click here to download (don't try to run it from current location). A fundamental article containing basic facts on discrete splines is here (scanned, 2.11 Mb). My implementation of the algorithm (F77 style subroutine KNOTINS.FOR) is also available. Self-explanatory comments included in the code. To write the main program you will need deBoor's collection of routines (or at least INTERV.FOR and BSPLVB.FOR) . An F77 style main program is written to show the usage of KNOTINS.FOR. A set for approximate algorithm for knot removal by Lyche and Morken is available as self-extractable file (F77 style routines); includes a postscript documentation of routines, and mathematics associated with the package will soon be available in T. Bosner's master thesis.
FURTHER RESEARCH, Seminars.
You can choose some of the subjects listed as a supplement to the exam, click here (in croatian)
Last updated: Tuesday, May 21, 2002