Odabrana poglavlja statistike u marketingu
Poglavlja:- Metoda glavnih komponenti (PCA)
- Eksploratorna faktorska analiza (EFA)
- Multidimenzionalno skaliranje (MDS)
- Linearna regresija (LM)
- Binarna klasifikacija (BK)
- Generalizirani linearni model (GLM)
- Hijerarhijski linearni modeli (HLM)
- Analiza korespodencije (AC)
Metoda glavnih komponenti (PCA) (slides)
- Primjer: Rscript podaci vizualizacija
To znači sljedeće. Varijabilitet brojeva ... \(\{x_{i1}, i=1,\ldots,m\}\) zapisanih u prvom stupcu matrice \(X\) (a to su projekcije točaka \(\{x^j, j=1,\ldots,p\}\) na prvu koordinatnu os) izražava se varijancom tih vrijednosti. Ako je vektor \(v\in\mathbb{R}^p\) neki vektor (kandidat) za novi koordinatni vektor (duljine 1), onda se računa varijanca brojeva \(\{x^j\cdot v, j=1,\ldots,p\}\) koji predstavljaju algebarske udaljenosti projekcija točaka \(x^j\) na \(v\)-os. To vodi na problem svojstvenih vrijednosti matrice kovarijanci \[C:=\frac{1}{m-1}\sum_{k=i}^m x_{ki}x_{kj}.\] Vektor \(v\) koji pripada maksimalnoj svojstvenoj vrijednosti od \(C\) dan je s \[ v:= {\text{argmax}}_{\|v\|=1} \langle Cv,v\rangle \] i to je svojstveni vektor od \(C\) koji pripada njenoj maksimalnoj svojstvenoj vrijednosti. To je ujedno prva glavna komponenta novog koordinatnog sustava. Na slici niže
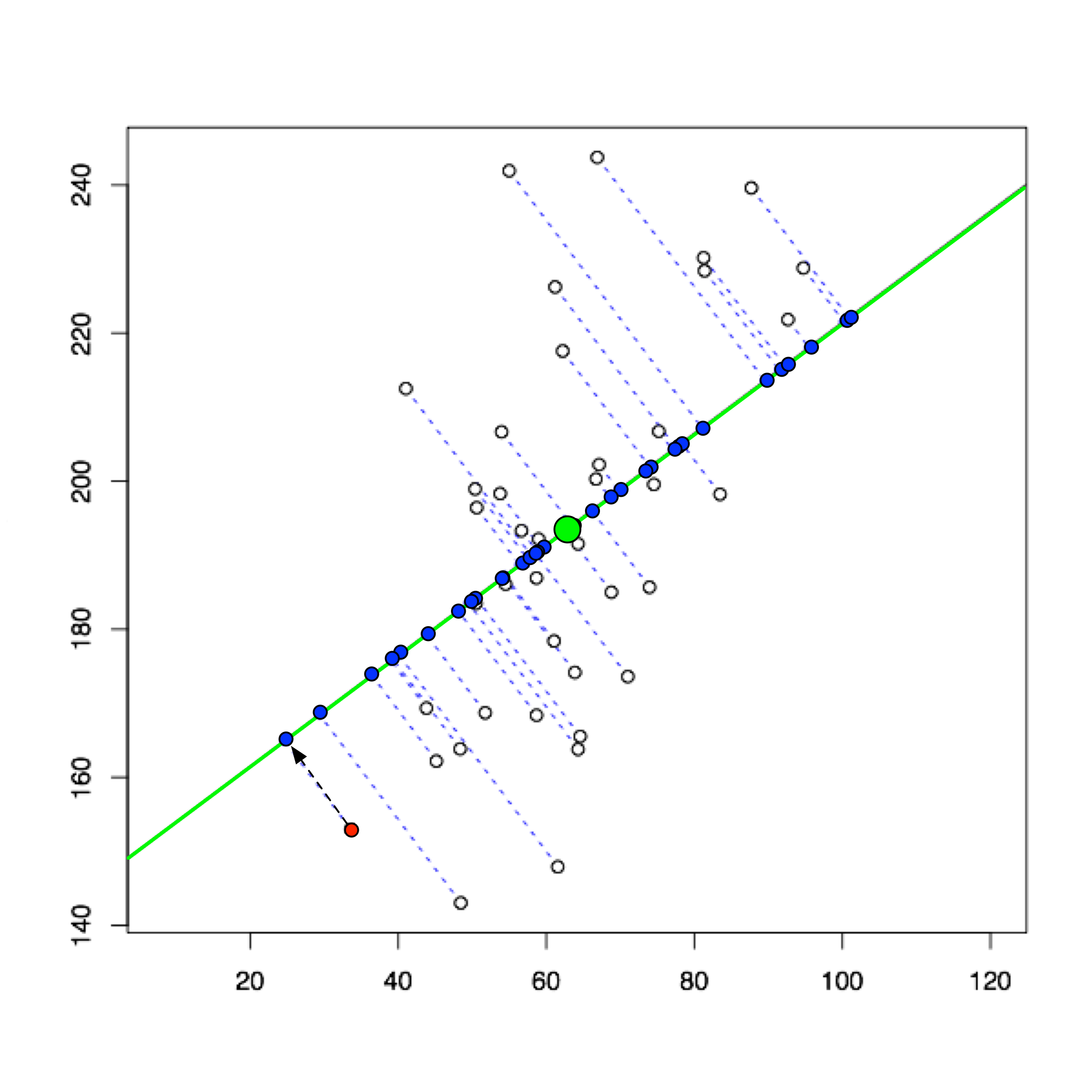
Nije teško zaključiti da je maksimizacija varijance jednaka minimizaciji kvadrata residuala koji su na slici predstavljeni kao udaljenosti točaka od osi.
Eksploratorna faktorska analiza (EFA) (slides)
Faktorska analiza (FA) donosi zaključke o latentnim (skrivenim, neuočljivim) varijablama kao što su: inteligencija, muzikalnost, navike potrošača... koje se ne mogu direktno mjeriti. Ona opisuje korelaciju među manifestinim varijablama \(X_1,\ldots, X_p\) u terminima manjeg broja latentnih faktora koji su uzrok varijabilnosti u podacima. Ortogonalni model ... povezuje faktore i manifestne varijable preko jednadžbi \begin{align} X_1 - \mu_1 & = \lambda_{11}F_1 + \lambda_{12}F_2 + \cdots \lambda_{1m}F_m + \epsilon_1 \notag\\ X_2 - \mu_2 & = \lambda_{21}F_1 + \lambda_{22}F_2 + \cdots \lambda_{2m}F_m + \epsilon_2 \notag\\ & \;\; \vdots \notag\\ X_p - \mu_p & = \lambda_{p1}F_1 + \lambda_{p2}F_2 + \cdots \lambda_{pm}F_m + \epsilon_p \notag\\[2ex] \lambda_{ij} & - \text{factor loading $i$-tog atributa}\notag \\ & \quad\; \text{na $j$-tom faktoru}\notag \\ \epsilon_i & - \text{nerastavljivi faktor (unique, specific)}\notag \end{align} ili u matričnom obliku \begin{align} \mathbb{R}^r\ni (X-\mu) & = \Lambda\cdot F + \epsilon. \label{eq:factor}\\ & \quad\, \uparrow \notag\\ \text{ matrica}& \text{ punjenja (loadings matrix)}\notag \end{align} Pretpostavke ortogonalnog modela: \begin{align} \bullet\ & E(F) = 0, \quad Var(F) = E(FF^\tau) = I \\ & \notag \text{Reskaliranjem faktora se može svesti na taj slučaj tako da to nije ograničenje} \\ \bullet\ &E(\epsilon) = 0, \quad Var(\epsilon) = E(\epsilon\epsilon^\tau ) = \Psi = diag(\psi_1,\ldots,\psi_p) \\ \bullet\ &F \text{ i } \epsilon \text{ su } \text{nekorelirane, tj. } Cov(F,\epsilon) = 0\\ \bullet\ &\text{Varijable $\epsilon_i$ nisu korelirane.} \end{align} Napomena. Nekoreliranost (ortogonalnost) faktora je zahtjev nepostojanja sinergije među njima (teško uhvatljiv pojam).Multidimenzionalno skaliranje (MDS) (slides)
MDS služi za redukciju dimenzije, a bazirano je na udaljenosti (sličnosti) među objektima. Klasičan primjer je odrediti (nacrtati) međusobni položaj gradova ako je zadana njihova međusobna udaljenost. Drugim riječima,- Traži se projekcija najmanjeg ranga koja čuva zadane udaljenosti.
- klasično MDS,
- metrijsko MDS,
- ne metrijsko MDS.
Fukciju \(d:S\rightarrow\mathbb{R}\) nazivamo metrikom ako zadovoljava aksiome: ...
- \(\forall x,y\in S,\; d(x,y)\ge0\) (pozitivnost)
- \(d(x,y)=0 \iff x=y\) (definitnost)
- \(\forall x,y\in S,\; d(x,y)=d(y,x)\) (simetričnost)
- \(\forall x,y,z\in S,\; d(x,z)\le d(x,y)+d(y,z).\) (tranzitivnost)
Zadan je konačan skup \(S\) i funkcija \(d:S\rightarrow\mathbb{R}\) koja zadovoljava pozitivnost i simetričnost (obično kao simetrična matrica \(D_{n\times n}\)). Naći \(x_1,\ldots x_n\in\mathbb{R}^p\) tako da je \(d_{ij} \approx \|x_i-x_j\|\).
Primjena:
Klasifikacija, strojno učenje, genetika, psihometrika,
neuroznanost (prepoznavanje: zvuka, slike)...
Doprinosi:
-
U kontekstu klasične diferencijalne geometrije:
Cayley (1841), Menger (1928), Fréchet (1935), Schoenberg (1935), Young-Householder (1938), Blumenthal (1938, 1953). -
Nemetričko skaliranje:
Stumpf (1880) promatra mjeru razlikovanja (dissimilarity), Thurstonova škola -- Messik & Abelson(1956), Coombs (1950), Kruskal (1973, 74) (nerazumljiv za tadašnje psihometričare (STRESS)), Tversky & Kranz (1968, 1970). -
Problem MDS sa šumom (probabilistic approach):
Borg & Groenen (1997), MacKay (1989), Steyvers & Busey (2000).
Zadan je konačni skup točaka \(S\subset\mathbb{R}^k\), \(n:=\#S\) s \(\ell_p\) metrikom. Tada je \(S\) izometrički smjestiv u \(\ell_p^N\) za \(N={n\choose2}\).
Problem je kako smanjiti dimenziju \(N\).
U praktičnim situacijama opravdano je zahtijevati da smještavanje
dozvoljava određenu \(\epsilon\)-distorziju metrike. To omogućava
niže dimenzije smještavanja.
Za općenite metričke prostore \((S, d)\) to nije uvijek moguće,
napr. ako je \(S\) jedinična sfera u \(\mathbb{R}^2\), a
\(d\) lučna metrika.
Klasično MDS. Postavljanje problema:
\[
X_{m\times p}=\left[
\begin{array}{ccc}
x_{11} & \cdots & x_{1p} \\
x_{21} & \cdots & x_{2p} \\
\vdots & \cdots & \vdots \\
x_{m1} & \cdots & x_{mp}
\end{array}
\right]
\xrightarrow { PCA }
Y=\left[
\begin{array}{ccc}
y_{11} & \cdots & y_{1p} \\
y_{21} & \cdots & y_{2p} \\
\vdots & \cdots & \vdots \\
y_{m1} & \cdots & y_{mp}
\end{array}
\right]
\]
Klasično MDS pretpostavlja da je \(D\) matrica euklidskih udaljenosti. Definirajmo: \(B=XX^\tau\). Pokazuje se da su \(B\) i \(D\) vezane, pa je ideja izraziti \(B\) preko \(D\) i zatim faktorizacijom dobiti \(X\) (Keller, 1958).
Donja slika pokazuje razliku između metrijskog i nemetrijskog MDS. (autor: Nelle Varoquaux)
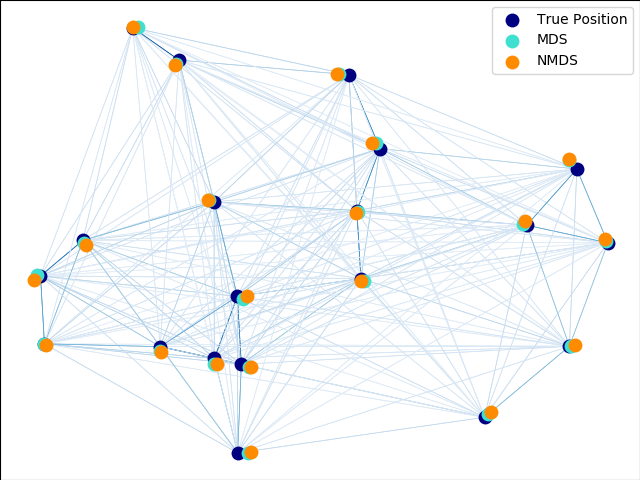
Linearna regresija (LM) (slides)
Literatura:Chris Chapman & Elea McDonnell Feit, R for Marketing Research and Analytics
Julian J. Faraway, Practical Regression and Anova using R, 2002
http://blog.minitab.com/blog/adventures-in-statistics/
R-podrška:
S predavanja. R-skripta (podaci)
Studentski radovi.
R-skripta (podaci)
R-skripta (podaci)
Model. \(y, x_1,\ldots,x_p, \epsilon\) slučajne varijable (\(y\) -- odzivna varijabla (response), \(x_i\) -- explanatorne varijable. Na primjer, \(x\) mogu biti historijski podaci kretanja cijena energenata na svjetskom tržištu, a \(y\) može biti kupovna moć izražena kao mjesečna potrošnja (po glavi stanovnika) određene košare osnovnih životnih namirnica u Hrvatskoj.
Ispitajmo model \[ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_px_p + \epsilon. \] Želimo procijeniti koeficijente ... \(\beta_i\). U tu svrhu mjerimo vrijednosti tih varijabli na uzorku subjekata \(S=\{s_1,\ldots,s_m\}:\) \[ y_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_px_{ip} + \epsilon_i, \; i= 1,\ldots,m \] Uvodimo oznake: \(Y=[y_i]^\tau\in\mathbb{R}^{m\times1}, \epsilon=[\epsilon_i]^\tau\in\mathbb{R}^{m\times1}\) \[ X = \left[ \begin{array}{ccccc} 1 & x_{11} & x_{12} & \cdots & x_{1p} \\ 1 & x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & x_{m1} & x_{m2} & \cdots & x_{mp} \\ \end{array} \right], \quad \beta = \left[ \begin{array}{c} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_m \end{array}\right] \] Jednadžbe pišemo u matričnoj formi \[ Y = X\beta + \epsilon, \qquad X - \text{dizajn matrica.} \] Geometrijska interpretacija.
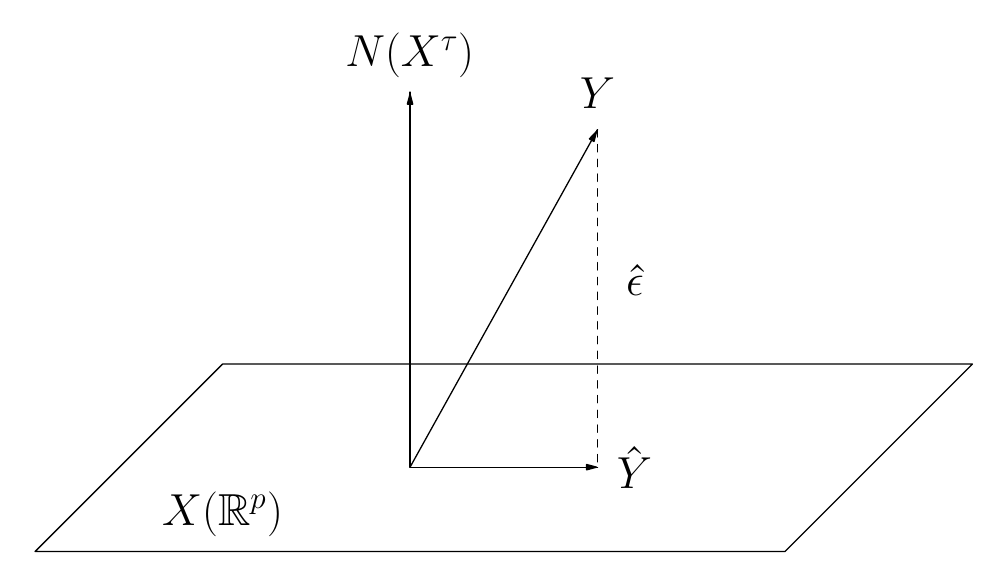
Neka je \(X\) realna matrica punog ranga po stupcima i \[ Y = X\beta + \epsilon \] gdje je očekivanje \(E(\epsilon)=0\) i \(Cov(\epsilon)=\sigma^2I_{m\times m}\). Tada \(\hat{\beta} = (X^\tau X)^{-1}Y\) ima majmanju kovarijancu (u odnosu na konus pozitivno semdefinitnih matrica) u klasi svih linearnih nepristranih procjena od \(Y\).
Binarna klasifikacija (BK) (slides)
Crtanje ROC krivulje.
R-skripta,
(podaci),
(dodatni podaci)

Problem spada u domenu strojnog učenja i danas je sastavni dio ... marketinških analiza. Varijabla kupnja je binarna.
Formulacija problema.
Za početak promatrajmo jednostavnije ulazne podatke.
| \( \begin{array}{ccc}%\hline X & Y & \hat{Y}\\\hline x_1 & 0 & \color{red}1\\ x_2 & 1 & \color{blue}1\\ x_3 & 0 & \color{blue}0\\ \vdots & \vdots & \color{blue}\vdots \\ x_m & 1 & \color{red}0 \end{array} \) |
|
Zbunj matrica (eng. confusion matrix).
| \[ \begin{array}{|c|cc|} \hline Y \backslash \hat{Y} & 1 & 0 \\ \hline 1 & \color{blue} {TP} &\color{red} {FN} \\ 0 & \color{red} {FP} & \color{blue} {TN} \\ \hline \end{array} \] | \[ \begin{array}{llll} \color{blue} {TP=n_{11}} & \color{blue}{\text{True Positive}} & \color{red} {FP=n_{21}} & \color{red} {\text{False Positive}} \\ \color{red} {FN=n_{12}} & \color{red} {\text{False Negative}} & \color{blue} {TN=n_{22}} & \color{blue}{\text{True Negative}} \\ \end{array} \] |
Kriterij optimalnosti \(x_0\) (preciznost).
\[ \frac{n_{11} + n_{22}}{n_{11} + n_{21} + n_{12} + n_{22}} \rightarrow\max. \] Spomenuti su još kriteriji: Youden, Fisher, McNemar, Barnard i DDIC (Descending Diagonal Intersection Criterion, (Leal, Oliviera, Sanchez (2012)).
Generalizirani linearni model (GLM) (slides)
Logistička krivulja. R-skripta.
Primjena (preživljavanje s Titanica). R-skripta (podaci)
Ne tako loš model. Jednostavnosti radi, promatrajmo jednu dihotomnu varijablu \(Y\) (bolest: da, ne) i jedan prediktor \(X\) (temperatura). Promatramo \begin{align} p(x) :=\;& P(Y=1|X=x) \label{eq:logit.Prob} \\ \text{i regresijski } & \text{ model ($z\in(-\infty,+\infty)$)}\\ z :=\;& \log\frac{p(x)}{1-p(x)} =\; \beta_0 + \beta_1 x + \epsilon. \label{eq:logit.model} \end{align} Zamjerka modelu: ... \(z\) ne poprima realne vrijednosti za \(p(x)=0\) i \(p(x)=1\). Ako je \(z\in\mathbb{R}\) i \(p_i\) u manjoj mjeri ovisno o \(i\) nema razloga ne koristiti ga.Logistička regresija. Ideja logističke regresije je da se umjesto gornjeg modela i metode najmanjih kvadrata promatra model \[ z :=\log\frac{p(x)}{1-p(x)} =\; \beta_0 + \beta_1 x \] (bez slučajne greške \(\epsilon\)) uz pretpostavku da je odzivna varijabla binomna, tj. \[ Y \sim B(1,p). \] Predikcija. Procijeniti \(p(x_i) := P(Y|X=x_i)\) kao funkciju od \(\theta=(\beta_0, \beta_1)\).
Učenje. Koeficijenti modela procjenjuju se maksimizacijom vjerodostojnosti (Vjerodostojnost danog uzorka je produkt individualnih vjerojatnosti): \begin{align} & \mathcal{L}(\theta) = \prod_{i=1}^n P(Y=y_i|X=x_i) = \prod_{i=1}^n p(x_i,\theta)^{y_i}(1-p(x_i,\theta)^{1-{y_i}})\\ &\text{gdje $y_i\in\{0,1\}$, a } p(x,\theta) = \frac{e^{\beta_0+\beta_1 x}}{1+e^{\beta_0+\beta_1 x}} = \Lambda(\beta_0 + \beta_1 x). \end{align}
To vodi na jednadžbe: \begin{align*} \sum_{y_i=1} (1-p_i) - \sum_{y_i=0} p_i &= 0\\ \sum_{y_i=1} (1-p_i) x_i - \sum_{y_i=0} p_ix_i &= 0, \end{align*} gdje je \begin{align*} p_i =\;& p(x_i,\theta)=\Lambda(z_i) \\ \Lambda(z) =\;& \frac{e^{z}}{1+e^{z}}. \end{align*} \(\Lambda\) je logistička funkcija koja je inverz od logit funkcije. Rješenja tih jednadžbi nije moguće dobiti u zatvorenoj formi već se rješavaju numerički Newtonovim iterativnim postupkom. Funkcija \(\Lambda(z)\) je kumulativna distribucija standardne logističke distribucije čija je gustoća \[ \lambda(z) = \frac{e^z}{(1+z)^2},\quad \mu=0,\quad \sigma=\frac{\pi^2}{3}. \]
Interpretacija modela.
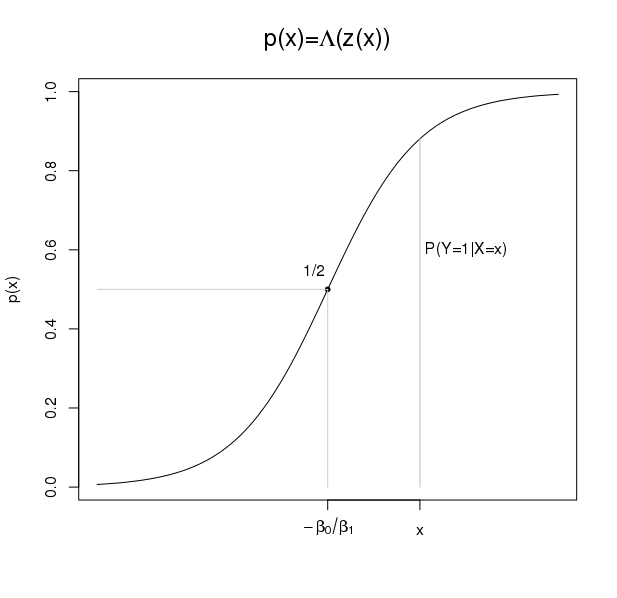
|
\begin{array}{@p{1in}} •\ \text{Točka infleksije od \(\Lambda\) je } z_i := -\frac{\beta_0}{\beta_1},\\ \quad\Lambda(z_i)=\frac{1}{2} \text{ (maks. separiranost),} \\ •\ \beta_1=0\Rightarrow \text{ omjer ne ovisi o } x, \\ •\ \exp(\beta_0)\cdot\exp(\beta_1) \text{ je promjena omjera}\\ \qquad \text{za jedinično povećanje } x, \\ •\ \text{Marginalni efekt od } p \text{ je: }\\ \quad p'(x) = \beta_1\Lambda'(z(x)) = \beta_1\Lambda(z)(1-\Lambda(z)). \end{array} |
Hijerarhijski linearni modeli (HLM) (slides)
Literatura:Chris Chapman & Elea McDonnell Feit, R for Marketing Research and Analytics
Woltman i dr. An introduction to hierarchical linear modeling
plotROC: A Tool for Plotting ROC Curves
Hijerhiska regresija vs. hierarchical model
Video:
Mixed Model Notation - A Simple Explanation
Radni primjer:
R-skripta (podaci) (Za objašnjenje podataka vidi: R for Marketing Research and Analytics)
Hijerarhijski grupirani ili ugnježđeni podaci su česta pojava. U obrazovnom okruženju na primjer, nositelji podataka su organizirani kao studenti, razredi, škole, regije...
U eksperimentima s ponovljenim mjerenjem nalazimo istu strukturu, možda manje evidentnu. Podaci se sakupljaju u raznim vremenima i pod različitim okolnostima. Njihovo agregiranje, upravo zbog različitih okolnosti pod kojima se vrše mjerenja, vodi ka osiromašenju podataka i gubljenju individualnosti.
Hijerarhijski linearni model (HLM) je dizajniran ... upravo za tako organizirane podatke. U suštini se radi o složenoj proceduri sumiranja u smislu najmanjih kvadrata koja se obavljaju po razinama (grupama). Na primjer, ako analiziramo uspjeh studenata, onda oni dijele varijabilnost te odzivne varijable i unutar razreda i unutar njihovih nastavnika (cross effect). Drugim riječima, uspjeh studenata ne ovisi samo o njemu već i o okruženju u kojem se nalazi i taj dio uspjeha je random effect.
Struktura podataka u HLM
.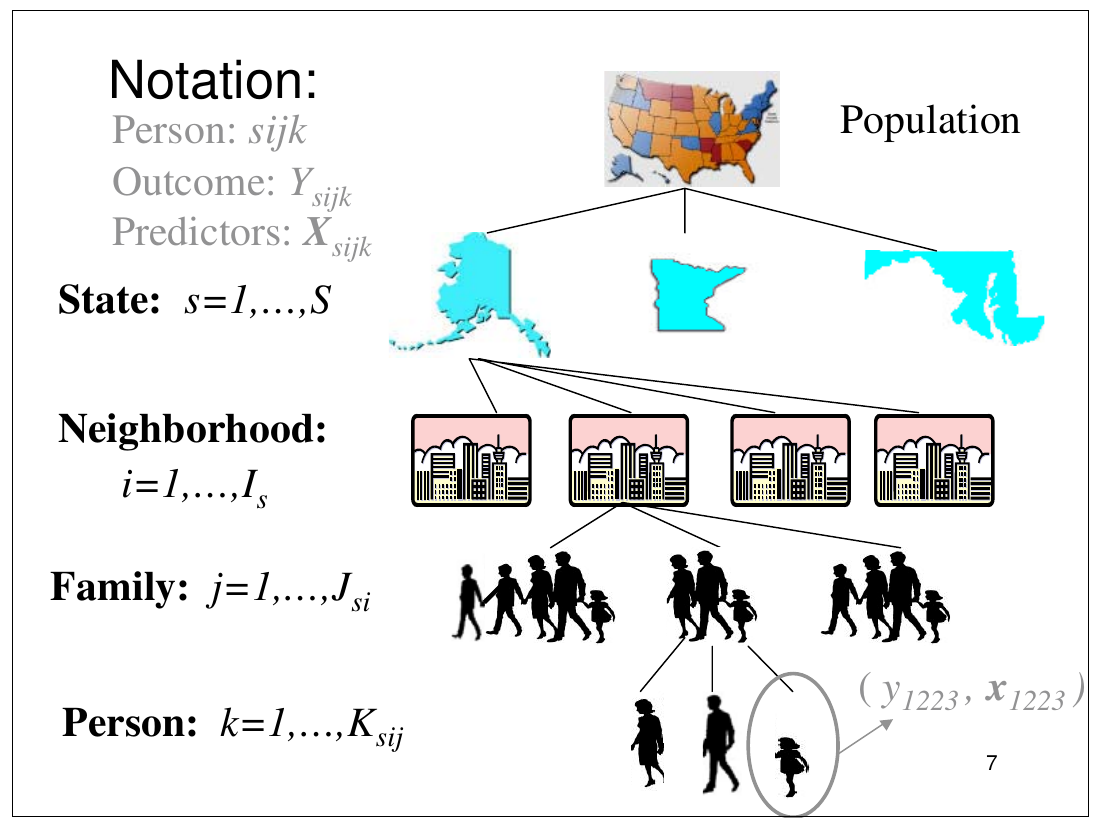
Nositelji informacija (entiteti):
- Učenici grupirani po razredima (učiteljima) u školama.
- Pacijenti grupirani po doktorima unutar klinika.
- Ponovljena mjerenja pojedinaca grupiranih po tretmanima (medicina, sport).
Varijable:
- Razina-1:
- spol (starost) učenika u razredu [ono po čemu se učenici razlikuju]
- Razina-2:
- tip (veličina) škole [ono po čemu se razlikuju škole]
Obrada ugnježđenih podataka.
- Razjedinjavanje
- Varijabla iz viših razina pridjeljuje objektima 1. razine vrijednosti pomoću usrednjavanja. Gubi se nezavisnost (varijabli).
- Ujedinjavanje
- Ignoriraju se razlike unutar grupe. Individua postaje homogeni entitet. Odzivna varijabla se agregira (upitna interpretacija)
- HLM
-
uočava i individualne i grupne efekte u odzivnoj varijabli
(varijabla 1. razine).
HLM je grupni naziv za više (sličnih) metoda koje u osnovi počivaju na metodi najmanjih kvadrata.
Sinonimi: {multilevel, mixed level, mixed effects, random effects}-modeling.
Organizacija HLM s dvije razine. Tipični ulazni podaci (data.frame):
|
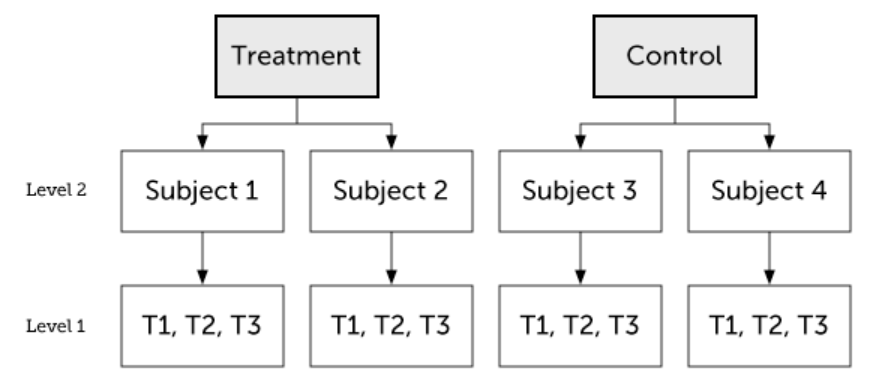
|
Slikovit prikaz organizacije hijerarhije i varijabli.
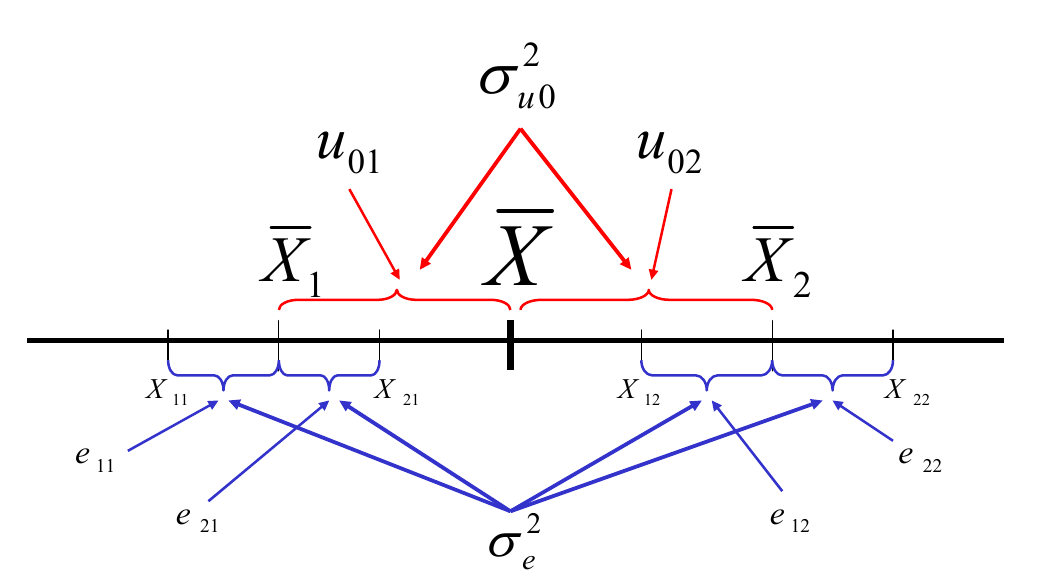
Implementacja.
# implementacija: R-kod
# lme4
# \gamma_{00} u_{0j}
# fixed effect random effect
# | |
lmer(y ~ 1 + ( 1 | id), data=data)
# nlme
lme(y ~ 1, random = ~ 1 | id, data=data)
Studentski zadatak:
R-kod (lme4) (podaci)
Analiza korespodencije (AC) (slides)
Literatura.Michael Greenacre, Correspondence Analysis in Practice
Greenacre, Nenadić, Correspondence Analysis in R. The ca Package
Greenacre, CA of the Spanish National Health Survey
Studentski radovi.
V. Jerebić, diplomski rad.
M. Cota, Biplot.
Primjeri.
Analiza ankete o osobnom osjećaju zdravlja. R-skripta (health-podaci, Greenacre)
Kosa-oči povezanost (R-skripta)
Metoda. U osnovi analize korespodencije (AC) stoji tablica kontingencije koja povezuje dvije kategorijske varijable na nekom skupu entiteta. U svakoj ćeliji te tablice stoji broj entiteta ... koji se svrstavaju u konkretnu kategoriju retka i konretnu kategoriju stupca. Analiza takve tablice provodi se AC analizom koja je sastavni dio nekoliko modula programskog paketa
R.
Za bolje razumijevanje širine primjene AC navodim jedan primjer iz biologije, u kojem se analizira rasprostranjenost nekih vrsta paukova u Hrvatskoj. Jedan mogući pristup je taj da se Hrvatska podijeli na staništa i za svako stanište izbroji se koliko paukova, od svake vrste, živi na tom staništu. Svako stanište ima svoje karakteristike koje ga određuju u kontekstu našeg problema. To može biti: (A) vlažnost tla, (B) vrsta tla, (C) dnevna/noćna prosječna temperatura, (D) nadmorska visina... Tablica kontingencije sadrži broj svake vrste pauka za svako stanište.
Cilj metode je vizualizirati podatke iz tablice, po mogućnosti na dvodimenzionalnoj slici, u kojoj je svaki redak biti reprezentiran točkom. To je kompleksna vizualizacija (biplot) elemenata iz različitih prostora: prostora redaka i prostora stupaca. Njihova međusobna udaljenost na slici nije interpretabilna, ali je intepretabilno nešto drugo. To su projekcije točaka-stupaca na os određenu točkom-retkom, i obratno, projekcije točaka-redaka na os određenu točkom stupcem. Redoslijed tih projekcija je ujedno i redoslijed stupnja 'naklonosti' odgovarajućih kategorija (retka) na os određenu konkretnim stupcem.
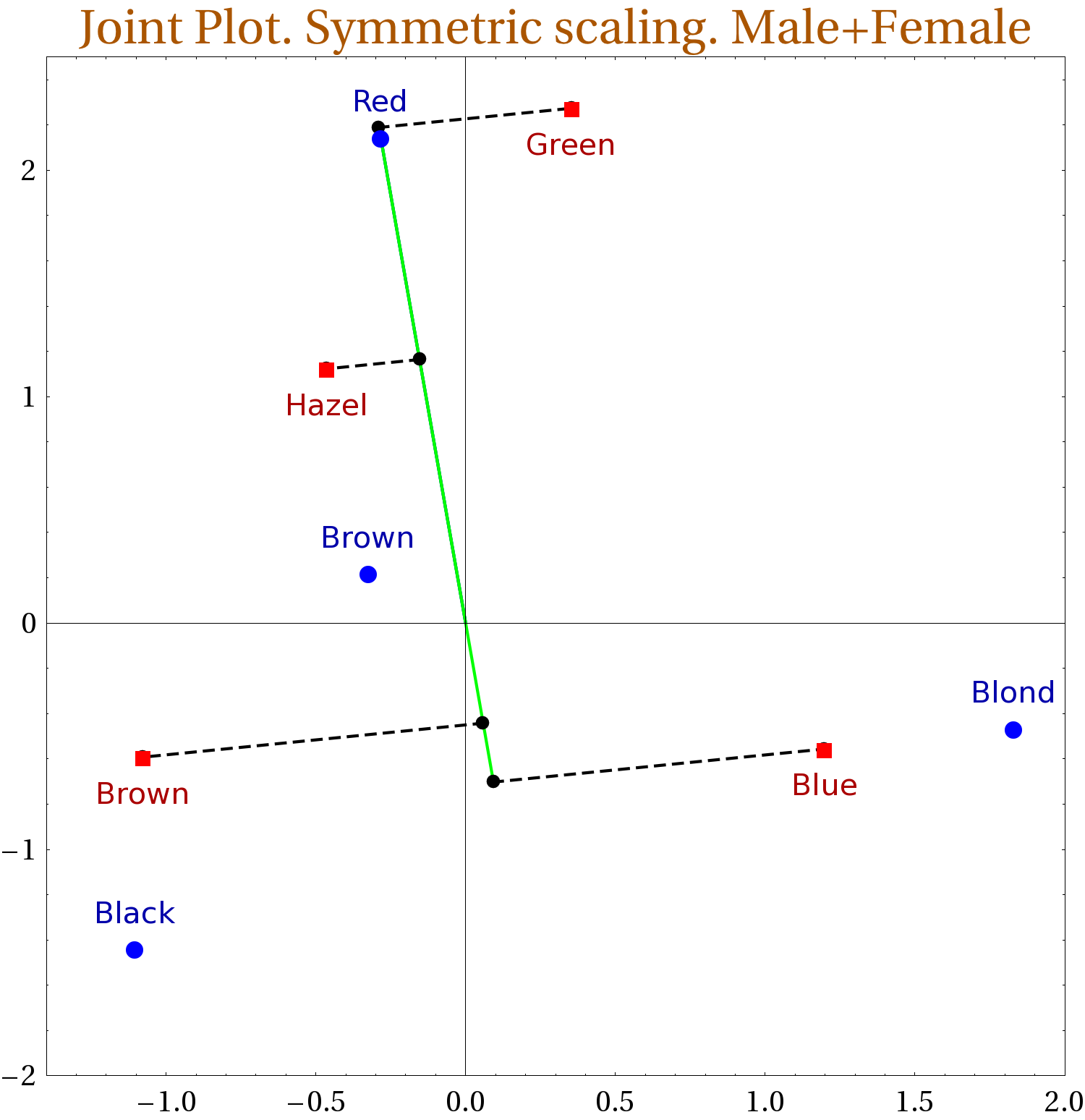
Teorija igara
Poglavlja:- Bimatrične igre (BM)
- Teoremi o nosaču (nosač)
- Neki važniji primjeri (primjeri)
- Nashova ravnoteža (Nash)
- Kritika (kritika)
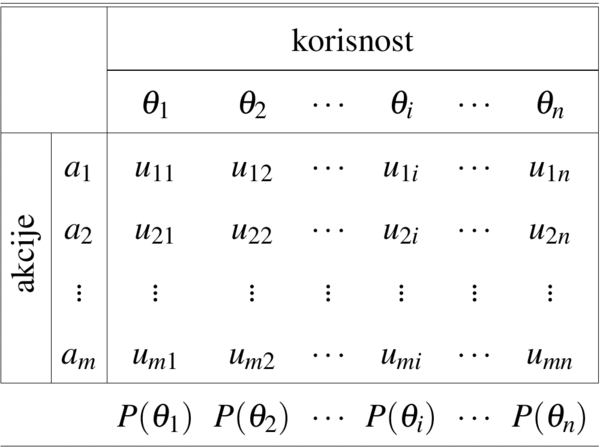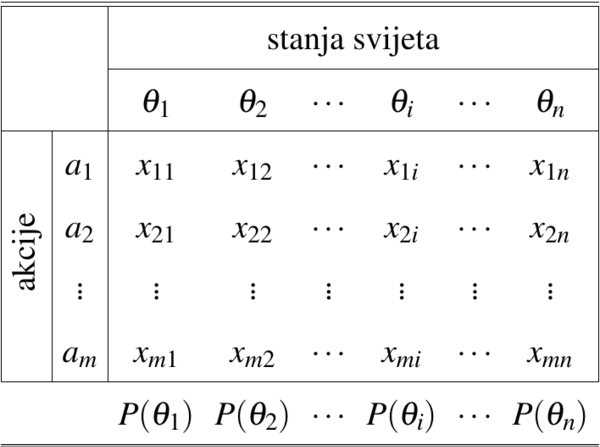
- Preferencije i korisnost (korisnost)
- Matrične igre (MI)
Slobodna definicija. Igra je interakcija između agenata (ljudi) u kojoj posljedice interakcije ovise o tome što agenti poduzimaju. Svaki sudionik igre vrednuje posljedice na nekoj skali zadovoljstva (korisnost). Igračima su postavljena ograničenja u vidu mogućih izbora njihovih akcija (pravila igre). Metode rješavanja ovise o ciljevima igre, ovisno o tome što igrači maksimiziraju: osobnu ili kolektivnu korisnost.
Bimatrične igre. Uvod. (slides)
Normalna (strateška) forma igre:| \[ \begin{array}{c|ccc|} & b_1 & b_j & b_n \\ \hline a_1 &&& \\ a_i & &(u,v)_{ij} & \\ a_m &&& \\ \hline \end{array} \] |
- Skup od dva igrača: \(\{A,B\}\),
-
\(S_A=\{a_1,\ldots, a_m\}\) i \(S_B=\{b_1, \ldots, b_n\}\)
---
akcije(strategije) igrača, -
uređen par \(\pi=(a,b),\; a\in S_A, b\in S_B\) ---
profil akcija (strategija), -
\(u, v:S_A\times S_B\rightarrow\mathbb{R}\) --- funkcije
korisnosti}(isplata) igrača. - Skraćeni zapis bimatrične igre je \((U,V)\) gdje su \(U,V\) matrice isplate.
\[ \begin{array}{c|ccc} & b_1 & &b_2 \\ \hline a_1 & (5,5)& \leftarrow & (3,2) \\ & \uparrow & & \updownarrow \\ a_2 & (3,2)& \leftarrow & (3,1) \end{array} \quad \text{alt. zapis} \quad \begin{array}{c|ccc} & b_1 & &b_2 \\ \hline a_1 & (5^*,5^*)& \phantom{\leftarrow} & (3^*,2) \\ & \phantom{\uparrow} & & \phantom{\uparrow} \\ a_2 & (3,2^*)& \phantom{\rightarrow} & (3^*,1) \end{array} \] Prvi stupac
jako dominira drugi stupac,
a prvi redak slabo dominira drugi redak, tj.
\(b_1>b_2\) (po komponentama) i \(a_1\ge a_2\) (po komponentama).
Definicija (Nashova ravnoteža)
Profil akcija \((a,b)\) je u ravnoteži ako \begin{align*} u(a,b) &\ge u(a,b'),\; \forall b'\in S_B, \\ v(a,b) &\ge v(a',b),\; \forall a'\in S_A. \end{align*}Nashova ravnoteža (NR) igre iz gornjeg primjera je profil akcija \((a_1, b_1)\). Akcije (strategije) još nazivamo
čistim strategijama.
Miješana strategija.
Miješana strategija igrača je vjerojatnostna distribucija
(stohastički vektor) na skupu mogućih izbora igrača.
Oznaka: \(\Sigma_A\) (za igrača \(A\)) i \(\Sigma_B\) (za igrača \(B\)).
Na taj način \(\Sigma_A\) postaje standardni simpleks dimenzije
\(m-1\) u prostoru jednostupčanih matrica \(\mathbb{R}^m\). Jednako
tako i za \(\Sigma_B\). Skup \(S_A\) (\(S_B\)) čistih strategija
možemo poistovjetiti sa skupom vrhova simpleksa \(\Sigma_A\)
(\(\Sigma_B\)).
Funkcije korisnosti \(u,v\) proširujemo na skup \(\Sigma_A\times\Sigma_B\) po bilinearnosti: \begin{align*} u(\sigma,\tau) =& \sum_{i=1}^m \sigma_iu_{ij}\tau_j, \\ v(\sigma,\tau) =& \sum_{i=1}^m \sigma_i v_{ij}\tau_j, \end{align*} Funkcije \(u, v\) nisu ništa drugo nego očekivane vrijednosti dvodimenzionalnih distribucija \(U=(u_{ij})\) i \(V=(v_{ij})\) s pripadnim vjerojatnostima \(u\) (\(v\)) od \((\sigma_i,\tau_j).\)
Definicija (Nashova ravnoteža)
Nashova ravnoteža je profil strategija
\((\sigma^*,\tau^*)\) koji zadovoljava
\begin{align*}
u(\sigma^*,\tau^*) &\ge u(\sigma^*,\tau), \forall \tau\in\Sigma_B, \\
v(\sigma^*,\tau^*) &\ge v(\sigma,\tau^*), \forall \sigma\in\Sigma_A.
\end{align*}
Drugim riječima, \((\sigma^*,\tau^*)\) je NR ako niti jedan igrač nema
poticaj mijenjati svoju odabranu strategiju uz pretpostavku da ni
ostali igrači to ne čine.
Zanimljivo je pitanje koji je najbolji odgovor igrača \(A\) na najbolji odgovor igrača $B$ na najbolji odgovor igrača \(A\) na najbolji odgovor ... To je jedno od centralnih pitanja u algoritamskoj teoriji igara poznato kao The best response mechanism. Odgovor nije nimalo jednostavan jer globalno rješenje ravnoteže \((\sigma^*,\tau^*)\) ne mora nužno biti limes lokalno pohlepnog algoritma: uzmi najbolji odgovor.
Igre s više od 2 igrača. Oznake
- Igrači
- \(\mathcal{I}=\{1,\ldots,n\}\) --- skup igrača, \(n\in\mathbb{N}\) --- broj igrača.
- Akcije
-
\(\Sigma_i\) --- skup (miješanih) strategija \(i\)-tog igrača.
\(\Sigma=\prod_{i=1}^n \Sigma_i\).
Za \(\sigma=(\sigma_1,\ldots,\sigma_n)\) pišemo \(\sigma_{-i}=(\sigma_1,\sigma_{i-1}, \sigma_{i+1},\sigma_n)\) i \(\sigma=(\sigma_i, \sigma_{-i})\).
Za \(a_i\in A_i\) je \(\sigma_i(a_i)\) --- vjerojatnost izbora akcije \(a_i\) u strategiji \(\sigma_i\). Čistu strategiju \(a\in A_i\) poistovjećujemo sa strategijom \(\sigma_i\in\Sigma_i\) za koju je: \(\sigma_i(a)=1\).
Skup \(\mathcal{supp}(\sigma):=\{a\in A\mid \sigma_i(a_i)>0\}\) ---nosačod \(\sigma\). - Korisnost
- Vektor korisnosti \(u=(u_1, \ldots, u_n)\) na \(A\) proširujemo po multilinearnosti na skup \(\Sigma\) formulom \begin{equation} u_i (\sigma) = \sum_{a\in A} u_i(a)\prod_{j=1}^n \sigma_j(a_j). \label{eq.korisnost} \end{equation} Očito je \(\sigma_i\mapsto u_i(\sigma_i, \sigma_{-i})\) linearna funkcija na \(\Sigma_i\).
- Najbolji odgovor
-
Maksimizacija (svoje) korisnosti je princip racionalnog igrača. Onaj
igrač koji se ne drži tog principa ne smatra se 'iracionalnim'. Za
svaku strategiju svojih suigrača, igrač traži takvu (svoju)
strategiju koja će mu donijeti najveću moguću korisnost. Takvu
strategiju nazivamo
najboljim odgovoromigrača za dane strategije suigrača.
Preciznije, \(\sigma_i\) je najbolji odgovor igrača \(i\) za strategije \(\sigma_{-i}\) svojih suigrača ako \[ u_i(\sigma_i,\sigma_{-i})\ge u(\tau,\sigma_{-i})\; \forall \tau\in\Sigma_i. \] Sve najbolje odgovore od \(\sigma_{-i}\) iznačimo s \(\psi_i{(\sigma_{-i})}\). Funkcija \(\sigma_{-i}\mapsto \psi_i{(\sigma_{-i})}\) je skupovna funkcija ilikorespodencija. Najbolji odgovor u pravilu nije jednoznačan. Označimo nadalje, \(\psi=\prod_i\psi_i\). Tada je \(\psi(\sigma)\subset\Sigma\) kartezijev produkt najboljih odgovora pojedinih igrača za profile njihovih suigrača.
Profil strategija \(\sigma\in\Sigma\) je Nashova ravnoteža ako \( \sigma\in\psi{(\sigma)}. \)Primjer.
| \[ \begin{array}{|c|c|c|c|} \hline & \text{L} & \text{C} & \text{R} \\ \hline U & 2,2 & 1^*,4^* & 4^*,4^* \\ \hline M & 3^*,3 & 1^*,0 & 1,5^* \\ \hline D & 1,1 & 0,5^* & 2,3 \\ \hline \end{array} \] | Najbolji odgovori: \begin{array}{ll} \psi_1{(L)}=\{M\} & \psi_1{(C)}=\{U,M\}, \\ \psi_1{(R)}=\{U\},& \psi_2{(U)}=\{C,R\}, \\ \psi_2{(M)}=\{R\},& \psi_2{(D)}=\{C\}. \end{array} |
\begin{align} U\in\psi_1{(C)}\; \&\; C\in\psi_2{(U)} &\; \Rightarrow (U,C) \text{ je NR}.\\ U\in\psi_1{(R)}\; \&\; R\in\psi_2{(U)} &\; \Rightarrow (U,R) \text{ je NR}. \end{align}
Teoremi o nosaču. (slides)
Teoremi o nosaču najboljeg odgovora.Teorem. Strategija \(\sigma_i\) je najbolji odgovor za \(\sigma_{-i}\) ako i samo ako je svaka čista strategija \(a_i\in A_i\) u nosaču od \(\sigma_i\) najbolji odgovor za \(\sigma_{-i}\).Posljedica toga je
Teorem (o nosaču u ravnoteži). Za svaku igru u strategijskoj formi, profil miješanih strategija \(\sigma^*\) je Nashova ravnoteža, ako i samo ako, za svakog igrača \(i\) vrijedi
- \(u_i(s_i, \sigma_{-i}^*) = u_i(s_i', \sigma_{-i}^*)\) za sve \(s_i, s_i'\in\mathit{supp}(\sigma_i^*)\)
- \(u_i(s_i, \sigma_{-i}^*) \ge u_i(s_i', \sigma_{-i}^*)\) za sve \(s_i\in\mathit{supp}(\sigma_i^*)\) i \(s_i'\not\in\mathit{supp}(\sigma_i^*)\).
Korolar. Ako je \(\sigma\) Nashova ravnoteža i ako je \(s_i\in A_i\) strogo dominirana čista strategija, tada \(s_i\) nije u nosaču od \(\sigma_i\).
Primjer (Iscrpno traženje najboljih odgovora). ...
\begin{array}{c|c|c|c|} & L & M & R \\ \hline U & 7,2 & 2,7 & 3,6 \\ \hline D & 2,7 & 7,2 & 4,5 \\ \hline \end{array} Prvo tražimo NR \(\sigma\) koja sadrži čiste strategije.
- korak 1)
- Najbolji odgovor za \(U\) je \(\{M\}\), ali najbolji odgovor za \(M\) je \(\{D\}\) koji ne sadrži \(U\). Dakle, \(U\) nije u nosaču od \(\sigma_1\).
- korak 2)
-
Najbolji odgovor za \(D\) je \(\{L\}\), ali najbolji odgovor za
\(L\) je \(\{U\}\) koji ne sadrži \(D\). Dakle, \(D\) nije u
nosaču od \(\sigma_1\).
Nosač od \(\sigma_1 = \{U, D\}\). - korak 3)
- Što se Stupca tiče, \(\sigma_2\) nema čistih strategija jer je skup najboljih odaziva za svaku čistu strategiju \(L,M,R\) jednočlan, a gore smo zaključili da \(\sigma_1\) ima nosač \(\{U,D\}\) koji je dvočlan.
- korak 4)
- Ispitujemo mogućnost \(\mathit{supp}(\sigma_2)=\{L,M,R\}\). \begin{array}{c|c|c|c|l} & {L} & {M} & {R} & \\ \hline U & 7,2 & 2,7 & 3,6 & x \\ \hline D & 2,7 & 7,2 & 4,5 & y=1-x \\ \hline \end{array} U tom slučaju je nužno \(u_2(\sigma_1,L)=u_2(\sigma_1,M)=u_2(\sigma_1,R)\) što vodi na inkonzistentan sustav \[ 2x+7y=7x+2y=6x+5y.\]
- korak 5)
- Ispitujemo mogućnost \(\mathit{supp}(\sigma_2)=\{L,M\}\). U tom slučaju je nužno \(u_2(\sigma_1,L)=u_2(\sigma_1,M)\) što vodi na sustav \[ 2x+7y=7x+2y \] čije je rješenje \(x=y=\frac{1}{2}\). Nadalje, \(u_1(U,\sigma_2)=u_1(D,\sigma_2)\), odnosno \(7\sigma_2(L)+2\sigma_2(M)=2\sigma_2(L)+7\sigma_2(M) \Rightarrow \sigma_2(L)=\sigma_2(M)=\frac{1}{2}\). Kandidat za NR je \(\sigma=(\frac{1}{2}U+\frac{1}{2}D,\frac{1}{2}L+\frac{1}{2}M)\) što je nemoguće jer je očekivana korisnost \(u_2(\frac{1}{2}U+\frac{1}{2}D,R)=\frac{11}{2}>\frac{9}{2}= u_2(\sigma)\).
- korak 6)
- Ispitujemo mogućnost \(\mathit{supp}(\sigma_2)=\{M,R\}\). Tada u odgovarajućoj subbimatrici \(D\) strogo dominira \(U\) što je u suprotnosti sa činjenicom da je \(u_1(U,\sigma_2)=u_1(D,\sigma_2)\).
- korak 7)
-
Ispitujemo mogućnost \(\mathit{supp}(\sigma_2)=\{L,R\}\). I Redak i
Stupac koriste miješane strategije, što znači da je
\begin{align*}
7\sigma_2(L)+3\sigma_2(R)&=2\sigma_2(L)+4\sigma_2(R) \Rightarrow \sigma_2(L)=\frac{1}{6}, \sigma_2(R)=\frac{5}{6} \\
2\sigma_1(U)+7\sigma_1(D)&=6\sigma_1(U)+5\sigma_1(D) \Rightarrow
\sigma_1(U)=\frac{1}{3}, \sigma_1(D)=\frac{2}{3}.
\end{align*}
Dakle, kandidat za ravnotežu je
\(\sigma=(\frac{1}{3}U+\frac{2}{3}D, \frac{1}{6}L+\frac{5}{6}R)\).
Ako je \(\sigma=(\frac{1}{3}U+\frac{2}{3}D, \frac{1}{6}L+\frac{5}{6}R)\) ravnoteža, onda nužno mora biti \begin{align*} u_2(\sigma) &\ge u_2(\sigma_1, M) \end{align*} tj. \(\frac{2}{18}+\frac{5\cdot6}{18}+\frac{2\cdot7}{18}+ \frac{10\cdot5}{18} = \frac{16}{3} \ge \frac{11}{3}=\frac{1\cdot7}{3} + \frac{2\cdot2}{3}\) što je istina. Dakle, \(\sigma\) je jedinstvena NR s isplatama \[ u_1(\sigma)=\frac{11}{3} \text{ i } u_2(\sigma)=\frac{16}{3}. \]
Time je iscrpno pretraživanje završeno.
Neki važniji primjeri (slides)
Navedeni su i riješeni primjeri nekih klasičnih diskretnih igara koje se pojavljuju u literaturi (rat spolova, dilema zatvorenika, napad-obrana, jastreb-golub, podjela ulova, racionalne svinje). Od beskonačnih igara obrađene su "tržišne igre" monopoly i duopoly.Nashova ravnoteža. Egzistencija (slides)
Teorem (Nash)... Teorem je dosta općenit i može se primijeniti na naš slučaj jer su funkcije \(u,v\) linearne u svakoj varijabli. Njegova je uporabnost ipak ograničena jer ne govori o tome koliko ima ravnoteža ni kako do njih doći. U literaturi ima puno dokaza Nashovog teorema i svi se baziraju na nekoj od tvrdnji koja je ekvivalentna Brouwerovom teoremu o fiksnoj točki. Osim Brouwerovog, teorem se najčešće dokazuje pomoću Kakutanijevog teorema o fiksnoj točki ili pomoću Ky Fanove nejednakosti.
Neka su \(\Sigma_i\subset\mathbb{R}^n\) konveksni kompaktni skupovi i \(u_i\) neprekidne funkcije na \(\Sigma\), \(i\in\mathcal{I}\). Pretpostavimo da je za svaki profil \(\sigma\in\Sigma\) skup točaka maksimuma funkcija \[ \sigma_{-i}\mapsto u_i(\sigma_i,\sigma_{-i}) \] konveksan. Tada igra \((\mathcal{I}, \Sigma, u)\) ima bar jednu Nashovu ravnotežu.
Kritika (slides)
Slaba uvjerljivost Nashove ravnoteže
1.\[ \begin{array}{c|c|c|c|} & {L} & {M} & {R} \\ \hline {U} & 1^*,1^* & 100^*,0 & -100,1^* \\ \hline {C} & 0,100 & 1,1 & 100^*,1 \\ \hline {D} & 1^*,-100 & 1,100^* & 1,1 \\ \hline \end{array} \] Jedinstvena ravnoteža igre je \((U,L)\). Redak može isti dobitak postići manje riskantnim izborom \(D\). Isto je i sa Stupcem. Zašto bi on igrao \(L\) kad bez rizika može postići isti dobitak igrajući \(R\)? Hoće li Nashovi sljedbenici isto tako zaključiti da je \((D,R)\) jednako racionalan izbor kao i \((U,L)\)?
Štoviše, u stvarnom životu, igrač može biti indiferentan na to je li njegov dobitak jednak \(1\) ili \(0\). U tom slučaju će Redak ... odabrati \(C\) jer može dobiti \(100\), a Stupac će odabrati \(M\) iz istog razloga, što završava isplatama \((1,1)\). Ova posljednja argumentacija je van matematičkog modela teorije igara jer igrači interno revidiraju svoje korisnosti i te informacije nisu dostupne suigraču.
2.
Preuzeto iz knjige Heap & Varoufakis, Game Theory: A Critical Introduction \[ \begin{array}{c|c|c|c|} & {L} & {M} & {R} \\ \hline {U} & {100}^*,99 & 0,0 & 99,{100}^* \\ \hline {C} & 0,0 & 1^*,1^* & 0,0 \\ \hline {D} & 99,{100}^* & 0,0 & {100}^*,99 \\ \hline \end{array} \qquad \begin{array}{c|c|c|c|} & {L} & {M} & {R} \\ \hline {U} & 2^*,1 & 0,0 & 1,2^* \\ \hline {C} & 0,0 & {1000}^*,{1000}^* & 0,0 \\ \hline {D} & 1,2^* & 0,0 & 2^*,1 \\ \hline \end{array} \] Igra lijevo i igra desno su jednako strukturirane. U svakoj su \(\{U\},\{C\},\{D\}\) najbolji odgovori za \(L, M, R\) respektivno i \(\{L\}, \{M\}, \{R\}\) su najbolji odgovori za \(D, C, U\) respektivno. Na prvi pogled, Nashova ravnoteža \((C,M)\) u igri desno čini se puno atraktivnijom nego u igri lijevo. J.K. Goeree & C.A. Holt su u nizu eksperimenata utvrdili različito ponašanje igrača u identično strukturiranim igrama s različitim isplatama.
3.
U sljedećoj igri postoje dvije NR: \((U,L)\) i \((C,M)\). Svaki od izbora \(U, C\) za retka i \(L,M\) za stupca, je riskantan zbog katastofalnih mogućih gubitaka. Ako se igrači ne koordiniraju gubici su neminovni. \[ \begin{array}{c|c|c|c|} & {L} & {M} & {R} \\ \hline {U} & 1^*,1^* & -10000,-10000 & 3^*,0 \\ \hline {C} & -10000,-10000 & {1}^*,{1}^* & 0,0 \\ \hline {D} & 0,3^* & 0,0 & 2,2 \\ \hline \end{array} \] Opcija \(D\) (\(R\)) čini se puno bolja zbog prihvatljivije distribucije isplata. Možemo li uvjerljivo tvrditi da je izbor \(D\) (\(R\)) "iracionalan"? Ako bi izbor \(D\) bio obostrano racionalan (ODR) onda bi Stupac birao \(L\), a Redak \(U\) zbog bolje isplate. Očito da strategija \(D\) nije dio niti jedne NR. Par \((\frac{2}{3}C+\frac{1}{3}D, \frac{2}{3}M+\frac{1}{3}R)\) je miješana ravnoteža koja dodatno komplicira nejedinstvenost NR.
Interpretacije randomizacije
Koncept miješane strategije čini se bizarnim u prvom trenutku. S matematičkog aspekta čini se razumno, ako igra nema ravnotežu među čistim strategijama, proširiti skup strategija i nadati se da će u većem skupu biti lakše pronači ravnotežu. Gledano geometrijski, miješane strategije nisu ništa drugo nego konveksifikacija skupa čistih strategija i predstavljaju njihovo prirodno proširenje.Stvarno pitanje je da li ljudi randomiziraju i kako?
U nekim situacijama to je prirodno. Na primjer, u stolnom tenisu postoje dva načina servisiranja: s rotacijom loptice i bez rotacije. Suigrač po načinu kretanja reketa protivnika trebao bi prepoznati kakav će biti servis i pravilno reagirati da ga loptica ne iznenadi. Igrač koji servisira namjerno randomizira da bi iznenadio protivnika.Pitanja koja se postavljaju su sljedeća: (1) postoji li način da se logički odrede vjerojatnosti u miješanoj ravnoteži i (2) da li randomizacija pomaže u rješavanju problema nejedinstvenosti NR.
Odgovor na oba pitanja je potvrdan ako se uvaži koncept Nashove ravnoteže. Na primjer, u igri rat spolova postoje dvije čiste ravnoteže: \((O,O)\) i \((N,N)\)
- (1) Indiferentnost.
- Niti jedan igrač nema razloga dati prednost nekoj od ravnoteža pa su indiferentni prema svojim strategijama.
- (2) Randomizacija.
- Ako su indiferentni onda mogu randomizirati, računati očekivane korisnosti i izjednačiti ih u skladu s (1).
- (3) Zaključak
-
Miješana strategija \(\sigma=(\frac{3}{5}O+\frac{2}{5}N,
\frac{2}{5}O+\frac{3}{5}N)\).
Preferencije i korisnost (u izradi)
Matrične igre (slides)
Definicija. Za danu bimatričnu igru \(((A,B),(u,v))\) kažemo da je matrična ako je \(u(x,y)=-v(x,y),\; x\in S_A, y\in S_B\).U matričnoj igri, jedan igrač dobiva onoliko koliko drugi gubi. To se može interpretirati kao da jedan igrač isplaćuje drugog. Matrična igra je jedinstveno određena matricom isplate \(U\) prvog igrača i \(u(x,y)=x^\tau Uy\).
Teorem (minmax, von Neumann). Neka je dana matrična igra s matricom isplate \(U\). Tada je \((\sigma^*,\tau^*)\) Nashova ravnoteža ako i samo ako \[ \min_\tau\max_\sigma u(\sigma,\tau) = u(\sigma^*,\tau^*) = \max_\sigma\min_\tau u(\sigma,\tau). \]Broj \(v:=u(\sigma^*, \tau^*)\) nazivamo vrijednošću igre.
Primjena $\min\!\max$ torema.
Grafičko računanje NR najlakše je ilustrirati na ... igrama tipa \(2\times n\) i \(m\times 2, m, n\ge 2\) pri čemu se koristi von Neumanov minmax teorem.U ovom primjeru matrica isplate je dana s \[ U= \left[ \begin{array}{ccc}2 & 1 \\ -1 & 2 \\ 1 & 1.5 \end{array} \right] \] Traži se Nashova ravnoteža \((\sigma,\tau)\).
Prema minmax teoremu (Oprez! Kada koristiti \(\min_y\max_x\), a kada \(\max_x\min_y\)) račun daje: \begin{align} v &=\min_y\max_x x^\tau Uy = \min_{y=[t\;1-t]^\tau}\max_{i\in\{1,2,3\}} \{e_i^\tau Uy\} \notag \\ &= \min_{t\in[0,1]}\max \left\{t+1, -3t+2, -\frac{1}{2}t+\frac{3}{2} \right\} = \frac{4}{3}, \label{eq.minmax} \end{align} a postiže se za \(t=\frac{1}{3}\) (skicirajte grafove). Dakle, \(\tau=[\frac{1}{3}\; \frac{2}{3}]^\tau\). Kako naći \(\sigma\)?
\[ U\tau = \frac{1}{3} \left[ \begin{array}{ccc}2 & 1 \\ -1 & 2 \\ 1 & 1.5 \end{array} \right] \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] = \frac{1}{3} \left[ \begin{array}{c} 4 \\ 3 \\ 4 \end{array} \right] =: U_\tau \] i iskoristimo činjenicu da je \[ \sigma^\tau U_\tau = v. \] Iskusan rješavatelj će uočiti da je \(\sigma(a_2)=0\) tj. da druga strategija prvog igrača nije u nosaču od \(\sigma\) (nije aktivna). Zaista, ako je \(\sigma=(\sigma_1, \sigma_2, \sigma_3)\) onda \begin{align*} \frac{4}{3} \sigma^\tau e - \sigma^\tau e_2 &= \frac{4}{3} \iff \sigma_2=0, \end{align*} gdje je (\(e=[1\;1\;1]^\tau\) stupac jedinica).
Iskoristimo neaktivnost \(\sigma_2\) i računamo NR reducirane matrične igre \(\widehat{U}\) bez drugog retka. Opet koristimo von Neumanov teorem (ovaj put \(\max\min\) verziju). \begin{align*} v= & \max_x\min_y x^\tau \widehat{U}y = \max_{x=[t\;1-t]} \min_{i\in\{1,2\}} \{ x^\tau \widehat{U}e_i\} \\ &= \max_t \left\{ t+1, -\frac{1}{2}t + \frac{2}{2} \right\} = \frac{4}{3}, \end{align*} a postiže se za \(t=\frac{1}{3}\). Dakle, \(\sigma=[\frac{1}{3}\;0\,\frac{2}{3}]^\tau\). Napomena. Matrica \(\widehat{U}\) je simetrična pa je moguće zaključiti \([\sigma_1\;\sigma_3]=\tau\) i korištenjem te simetrije.
\(\mathit{Minmax}\) zapis u formi \[ \min_{t\in[0,1]} \max \left\{t+1, -3t+2, -\frac{1}{2}t+\frac{3}{2} \right\} = \frac{4}{3} \] ima grafički prikaz u kojem su nacrtani pravci: \(y=t+1, y=-3t+2\) i \(y=-\frac{1}{2}t+\frac{3}{2}\), a crvenom bojom je nacrtana max-envelopa tih pravaca. Minimum te envelope postiže se za vrijednost \(t^*=\frac{1}{3}\) i iznosi \(v=\frac{4}{3}\). Dakle, \[ \tau=\left[\frac{1}{3}\;\; \frac{2}{3}\right]^\tau. \]
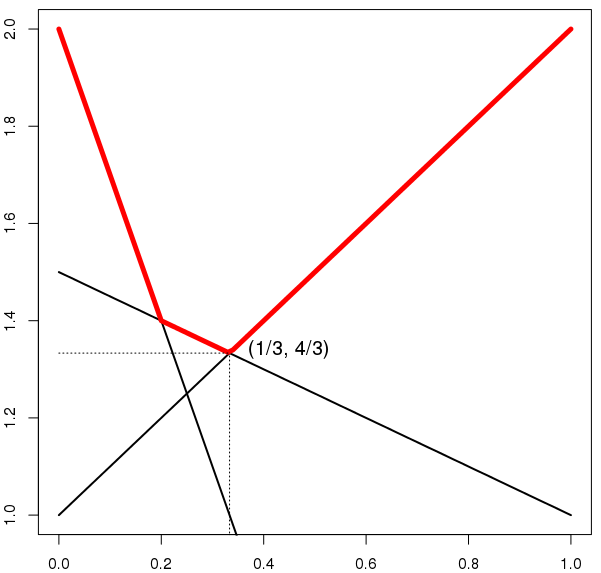
Aktivne komponente (u nosaču) od \(\sigma\) su određene pravcima koji prolaze točkom \((\frac{1}{3}, \frac{4}{3})\) su \(\{1, 3\}\), što znači da su to prvi i treći pravac.
Rješenje matrične igre
Neka su $\Sigma_1, (\Sigma_2)$ -- miješane strategije prvog (drugog) igrača. Rješenje matrične igre \(A\in\mathbb{R}^{n\times n}\) je uređena trojka \((\bar{x}\in\Sigma_1, \bar{y}\in\Sigma_2,v\in\mathbb{R})\) takva da vrijedi \begin{align} \bar{x}^\tau A y & \ge v, \;\forall y\in\Sigma_2 \label{eq.v+}, \tag{1} \\ x^\tau A \bar{y} & \le v, \; \forall x\in\Sigma_1 \label{eq.v-}, \tag{2} \\ v &= \bar{x}^\tau A\bar{y} . \label{eq.v=} \tag{3} \end{align}Ako je \((\bar{x}, \bar{y})\) Nashova ravnoteža matrične igre onda je \((\bar{x}, \bar{y},\bar{x}^\tau A\bar{y} )\) rješenje i obratno.
Geometrijska interpretacija. Označimo s $1\!\!1$ stupac jedinica i \(C_v, H\subset\mathbb{R}^n\) \begin{align} C_v := & \{\ x\in\mathbb{R}^n \mid x\le v\cdot1\!\!1 \}, \quad\text{(konus)} \\ H=H_{\bar{x},v} := & \{\ x\in\mathbb{R}^n \mid \bar{x}^\tau x = v \} \quad\text{(hiperravnina)}. \end{align} Očito je \(C_v\subseteq H^-\), \eqref{eq.v+} znači da je politop generiran stupcima matrice \(A\) podskup poluprostora \(H^+\), a \eqref{eq.v-} i \eqref{eq.v=} povlače da je \(A\bar{y}\in C_v\cap H\) (zadatak).