Glasnik Matematicki, Vol. 45, No.1 (2010), 43-53.
ON (m, n)-JORDAN CENTRALIZERS IN RINGS AND
ALGEBRAS
Joso Vukman
Department of Mathematics and Computer Science,
University of Maribor, FNM, Koroska 160, 2000 Maribor, Slovenia
e-mail: joso.vukman@uni-mb.si
Abstract. Let m ≥ 0, n ≥ 0 be fixed integers with
m+n ≠ 0
and let R be a ring. It is our aim in this paper to investigate
additive mapping
T : R → R satisfying the relation
(m+n)T(x2) = mT(x)x +
nxT(x) for all
x 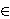 R.
R.
2000 Mathematics Subject Classification.
16W10, 46K15, 39B05.
Key words and phrases. Ring, prime ring, semiprime ring, Banach
space, Hilbert space, algebra of all bounded linear operators, standard
operator algebra, H*-algebra, derivation, Jordan derivation, left
(right) centralizer, two-sided centralizer, left (right) Jordan centralizer,
(m,n)-Jordan centralizer.
Full text (PDF) (free access)
DOI: 10.3336/gm.45.1.04
References:
- W. Ambrose,
Structure theorems for a special class of
Banach algebras, Trans. Amer. Math. Soc. 57 (1945), 364-386.
MathSciNet
CrossRef
- K. I. Beidar, W. S. Martindale III and A. V. Mikhalev,
Rings with generalized identities, Marcel Dekker, Inc., New York, 1996.
MathSciNet
- M. Bresar and J. Vukman,
Jordan derivations on prime
rings, Bull. Austral. Math. Soc. 37 (1988), 321-323.
MathSciNet
CrossRef
- M. Bresar,
Jordan derivations on semiprime rings,
Proc. Amer. Math. Soc. 104 (1988), 1003-1006.
MathSciNet
CrossRef
- M. Bresar,
Jordan mappings of semiprime rings,
J. Algebra 127 (1989), 218-228.
MathSciNet
CrossRef
- M. Bresar and B. Hvala,
On additive maps of prime rings, II, Publ. Math. Debrecen 54 (1999), 39-54.
MathSciNet
- J. Cusack,
Jordan derivations on rings, Proc. Amer. Math.
Soc. 53 (1975), 321-324.
MathSciNet
CrossRef
- I. N. Herstein,
Jordan derivations in prime rings, Proc.
Amer. Math. Soc. 8 (1957), 1104-1110.
MathSciNet
CrossRef
- L. Molnár,
On centralizers of an H*-algebra,
Publ. Math. Debrecen 46 (1995), 89-95.
MathSciNet
- I. Kosi-Ulbl and J. Vukman,
On centralizers of standard
operator algebras and semisimple H*-algebras, Acta Math. Hungar.
110 (2006), 217-223.
MathSciNet
CrossRef
- J. Vukman,
An identity related to centralizers in
semiprime rings, Comment. Math. Univ. Carolin. 40 (1999), 447-456.
MathSciNet
- J. Vukman and I. Kosi-Ulbl,
Centralizers on rings and
algebras, Bull. Austral. Math. Soc. 71 (2005), 225-234.
MathSciNet
CrossRef
- J. Vukman and I. Kosi-Ulbl,
On centralizers of semisimple H*-algebras,
Taiwanese J. Math. 11 (2007), 1063-1074.
MathSciNet
- B. Zalar,
On centralizers of semiprime rings, Comment.
Math. Univ. Carolin. 32 (1991), 609-614.
MathSciNet
Glasnik Matematicki Home Page
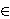 R.
R.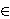 R.
R.