Glasnik Matematicki, Vol. 44, No.2 (2009), 447-455.
ON SOME FUNCTIONAL EQUATIONS ON STANDARD
OPERATOR ALGEBRAS
Irena Kosi-Ulbl and Joso Vukman
Faculty of Mechanical Engineering, University of Maribor, Smetanova ul. 17, Maribor, Slovenia
e-mail: irena.kosi@uni-mb.si
Department of Mathematics and Computer Science, FNM, University of Maribor,
Koroska 160, Maribor, Slovenia
e-mail: joso.vukman@uni-mb.si
Abstract. The main purpose of this paper is to prove the following
result. Let X be a real or complex Banach space, let L(X) be the algebra
of all bounded linear operators on X, let
A(X) 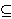 L(X) be a
standard operator algebra, and let
T : A(X) → L(X) be an additive
mapping satisfying the relation
T(A2n+1) = ∑i=12n+1
(-1)i+1 Ai-1 T(A)
A2n+1-i,
for all A
L(X) be a
standard operator algebra, and let
T : A(X) → L(X) be an additive
mapping satisfying the relation
T(A2n+1) = ∑i=12n+1
(-1)i+1 Ai-1 T(A)
A2n+1-i,
for all A 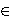 A(X)
and some fixed integer n ≥ 1. In this case T\ is of the form
T(A) = AB + BA, for all
A
A(X)
and some fixed integer n ≥ 1. In this case T\ is of the form
T(A) = AB + BA, for all
A 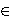 A(X) and some fixed
B
A(X) and some fixed
B 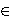 L(X). In particular,
T is continuous.
L(X). In particular,
T is continuous.
2000 Mathematics Subject Classification.
46K15, 39B05.
Key words and phrases. Prime ring, semiprime ring, Banach space,
standard operator algebra.
Full text (PDF) (free access)
DOI: 10.3336/gm.44.2.11
References:
- K. I. Beidar, W. S. Martindale III and A.V. Mikhalev,
Rings with generalized identities, Marcel Dekker, Inc. New York, 1996.
MathSciNet
- K. I. Beidar, M. Bresar, M.A. Chebotar and W. S. Martindale 3 rd,
On Herstein's Lie map conjectures II, J. Algebra 238
(2001), 239-264.
MathSciNet
CrossRef
- P. R. Chernoff,
Representations, automorphisms, and
derivations of some operator algebras, J. Functional Analysis 12 (1973), 275-289.
MathSciNet
CrossRef
- J. Cusack,
Jordan derivations on rings, Proc. Amer. Math.
Soc. 53 (1975), 321-324.
MathSciNet
CrossRef
- M. Fosner and D. Ilisevic,
On a class of
projections on *-rings, Commun. Algebra 33 (2005), 3293-3310.
MathSciNet
CrossRef
- M. Fosner and J. Vukman,
On some equations in prime
rings, Monatsh. Math. 152 (2007), 135-150.
MathSciNet
CrossRef
- I. N. Herstein,
Jordan derivations of prime rings, Proc.
Amer. Math. Soc. 8 (1957), 1104-1110.
MathSciNet
CrossRef
- G. N. Jacobson,
Structure of rings, American Mathematical
Society, New York, 1956.
MathSciNet
- I. Kosi-Ulbl and J. Vukman,
An identity related to
derivations of standard operator algebras and semisimple H*-algebras,
CUBO A Math. J., to appear.
- L. L. Stachó and B. Zalar,
Bicircular projections on
some matrix and operator spaces, Linear Algebra Appl. 384 (2004), 9-20.
MathSciNet
CrossRef
- L. L. Stachó and B. Zalar,
Bicircular projections and
characterization of Hilbert spaces, Proc. Amer. Math. Soc. 132 (2004),
3019-3025.
MathSciNet
CrossRef
- P. Semrl,
Ring derivations on standard operator
algebras, J. Funct. Anal. 112 (1993), 318-324.
MathSciNet
CrossRef
- J. Vukman,
On automorphisms and derivations of operator
algebras, Glasnik Mat. Ser. III 19(39) (1984), 135-138.
MathSciNet
- J. Vukman, I. Kosi-Ulbl and D. Eremita,
On certain
equations in rings, Bull. Austral. Math. Soc. 71 (2005), 53-60.
MathSciNet
CrossRef
- J. Vukman,
On functional equations related to bicircular
projections, Glasnik Mat. Ser. III 41(61) (2006), 51-55.
MathSciNet
CrossRef
- J. Vukman,
On derivations of standard operator algebras
and semisimple H*-algebras, Studia Sci. Math. Hungar. 44
(2007), 57-63.
MathSciNet
CrossRef
Glasnik Matematicki Home Page
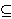 L(X) be a
standard operator algebra, and let
L(X) be a
standard operator algebra, and let
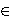 A(X)
and some fixed integer n ≥ 1. In this case T\ is of the form
T(A) = AB + BA, for all
A
A(X)
and some fixed integer n ≥ 1. In this case T\ is of the form
T(A) = AB + BA, for all
A 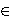 A(X) and some fixed
B
A(X) and some fixed
B 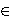 L(X). In particular,
T is continuous.
L(X). In particular,
T is continuous.
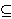 L(X) be a
standard operator algebra, and let
L(X) be a
standard operator algebra, and let
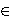 A(X)
and some fixed integer n ≥ 1. In this case T\ is of the form
T(A) = AB + BA, for all
A
A(X)
and some fixed integer n ≥ 1. In this case T\ is of the form
T(A) = AB + BA, for all
A 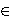 A(X) and some fixed
B
A(X) and some fixed
B 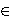 L(X). In particular,
T is continuous.
L(X). In particular,
T is continuous.